图文推荐
-

网上真人百家乐游戏玩法介绍
分类:百家乐游戏 关注:89次
网上真人百家乐游戏玩法介绍 游...[详细]
-

真人牌九游戏玩法技巧
分类:温州牌九游戏 关注:160次
网上真人牌九游戏玩法规则介绍...[详细]
-
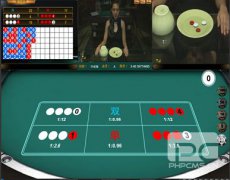
真人色碟游戏玩法规则介绍
分类:色碟游戏 关注:58次
bbin波音游戏平台,真人 色碟游戏...[详细]
-

真人牛牛游戏玩法,牛牛游戏技巧
分类:牛牛游戏 关注:66次
真人 牛牛游戏玩法, 牛牛游戏技...[详细]
-

bbin波音平台,真人21点游戏玩法规则介绍
分类:其他博彩游戏 关注:108次
游戏目的是取得越接近21点且不超...[详细]
-

欧式21点游戏玩法规则
分类:其他博彩游戏 关注:89次
21点源于法国,只要玩家的扑克牌...[详细]
-

网上真人竞咪百家乐游戏玩法规则
分类:百家乐游戏 关注:158次
竞咪百家乐 网上真人竞咪百家乐...[详细]
-

真人包桌百家乐游戏规则
分类:百家乐游戏 关注:86次
包桌百家乐 下注模式: 包桌(...[详细]
-

龙宝百家乐游戏玩法介绍
分类:其他博彩游戏 关注:104次
龙宝百家乐 龙宝会根据所投注一...[详细]
-

真人游戏,保险百家乐游戏玩法介绍
分类:其他博彩游戏 关注:118次
保险百家乐 保险百家乐是近年最...[详细]
-

波音平台真人德州扑克游戏介绍
分类:德州扑克游戏 关注:102次
德州扑克 德州扑克Texas Holdem,使...[详细]
-

网上真人鱼虾蟹游戏玩法介绍
分类:其他博彩游戏 关注:181次
网上真人鱼虾蟹游戏 鱼虾蟹,又...[详细]
-

网上真人番摊游戏介绍
分类:其他博彩游戏 关注:64次
网上真人番摊游戏介绍 游戏简介...[详细]
-

网上真人21点游戏介绍
分类:其他博彩游戏 关注:194次
网上真人21点游戏介绍 游戏简介...[详细]
-

网上真人牛牛游戏介绍
分类:牛牛游戏 关注:94次
网上真人牛牛游戏介绍 游戏简介...[详细]
-

网上真人色碟游戏介绍
分类:色碟游戏 关注:123次
网上真人色碟游戏介绍 游戏简介...[详细]











